El dilema de Tarzán (2ª parte)

Una vez planteado el problema al que debe enfrentarse el Rey de los Monos, el siguiente paso lógico consiste en calcular la distancia horizontal de un proyectil que ha sido lanzado desde lo alto de un acantilado, por ejemplo, es decir, desde un punto situado a una altura H sobre el suelo (quizá algunos profesores ya hayan realizado este ejercicio elemental en sus clases, con lo que sus estudiantes podrán comprobar su utilidad en el presente desafío).

Si se utilizan las técnicas habituales en el estudio de la cinemática del movimiento parabólico y se plantean sendas ecuaciones correspondientes a ambas coordenadas (horizontal y vertical) tal y como se han visto en el aula, la expresión que se obtiene para dicha distancia máxima horizontal es:

Es fácil comprobar que la expresión anterior se reduce a la muy conocida

si se calcula el límite de aquella cuando H tiende a cero, lo cual puede reforzar la confianza de los estudiantes y animarles a continuar con la pequeña investigación que han emprendido, además de proporcionarles la oportunidad de repasar el concepto de límite de una función, así como la relación del seno del ángulo doble.

De la primera ecuación se pueden sacar conclusiones muy interesantes, tales como:

1.- El ángulo óptimo para lograr que la distancia alcanzada por el proyectil sea máxima puede calcularse de la forma habitual, es decir, hallando la derivada con respecto al ángulo e igualando a cero. Obviamente, esto resulta algo más engorroso que para el caso elemental en que los puntos de lanzamiento y de impacto se encuentran sobre la misma horizontal, en cuyo caso ya habíamos dicho que el ángulo óptimo era de 45°.

2.- Si se procede a representar gráficamente (aquí puede ser de ayuda algún software específico como Mathematica, Maple, Excel, etc.) el resultado teórico y prestando atención se deduce que el ángulo óptimo de lanzamiento es tanto menor cuanto mayor sea la altura del acantilado, H.

3.- Por tanto, si el acantilado es muy alto, el lanzamiento de máxima distancia se acerca mucho a un tiro horizontal, esto es, con theta = 0.

Hasta aquí, todo lo que necesitamos para resolver el dilema de Tarzán que nos habíamos planteado al principio. Veamos, si os habéis dado cuenta, aún no conocemos el valor de la velocidad del hombre-mono justo en el momento en que suelta la liana (esto es, la velocidad inicial v₀ con la que se efectúan los lanzamientos parabólicos). Una excelente oportunidad para recordar el principio de conservación de la energía mecánica:

y como se puede ver en la figura 

entonces se puede escribir lo siguiente:

Ahora, si sustituimos este valor en la primera de las ecuaciones, la de arriba del todo, tendremos la máxima distancia alcanzada por Tarzán, siempre que la midamos desde el punto en el que éste suelta la liana. En cambio, si deseamos saber la distancia total, medida desde el punto en el que Tarzán agarra la misma liana en posición vertical, tan sólo debemos sumar a la cantidad anterior L sin(theta), como fácilmente se deduce de la figura de arriba. Finalmente,

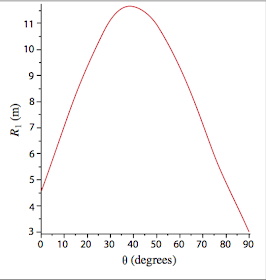
La mejor forma de escudriñar la expresión anterior consiste en hacer una representación gráfica de la misma, situando el ángulo en abscisas y la distancia alcanzada por Tarzán en ordenadas. Así, para unos valores numéricos de lo más razonables como pueden ser una velocidad en carrera para nuestro héroe de 36 km/h, una liana de 3 metros de longitud situada a una altura de 1 metro sobre el suelo, el ángulo óptimo resulta ser de algo más de 39° (ver dibujo bajo estas líneas).

(Continuará...)